概要
TQQQでケリー基準に従って取引した場合の資産推移について、検討しました。
シミュレーション1
確定利益率を変えながらケリー基準に従った取引のシミュレーションを行いました。
計算方法
- 投資対象:TQQQ
- 計算期間:2011年1月初めから2020年12月末まで
- TQQQの価格は始値->(高値or安値で始値に近い側)->(高値or安値で始値から遠い側)->終値で推移すると仮定。1分足データが入手できないため。
- ETF購入後、利確率まで上昇すれば、利益確定、損切率まで下落すれば損切する、を繰り返す。
- その際の1回あたりの掛け金はケリー基準に従う
- 確定後、翌日の始値で再度購入するとする。
- スプレッドは買い・売りともに0.03%とする。
- 利確率Rp, 損切率Rlを設定する。0.05(5%)から1(100%)まで、0.05(5%)刻みで検討する。
- 損切あり、損切なしの場合両方について検討する。
- 損切ありの場合Rp=Rlとする。例えば、Rp=0.05( 5%), Rl= 0.05(5%)とする。
- 10年間繰り返した場合の勝敗記録から、それぞれの利確率、損切率の組み合わせについて、勝率pを求める(価格推移はランダムとされているので、得られた勝敗から勝率を求めても良いと考えている)。
- 勝率pからoptimal f, f= ((Rp+ 1) * p – 1) / Rlを求める。
- optimal fから1回あたりの最適掛け金を求める。
- 上記の場合での資産推移S(f)を確認する。
取引回数
下記グラフは損切あり、損切なしでの取引回数です。
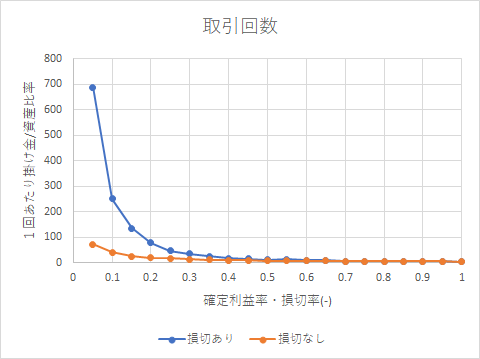
損切なし、確定利益率0.1のとき、取引回数は約40回/10年なので、3か月に1回程度になります。
勝率
下記グラフは損切あり、損切なしでの勝率です。
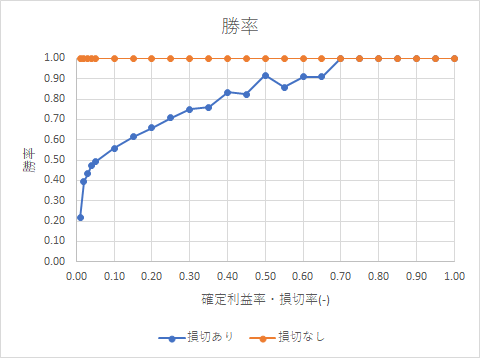
損切ありの場合、確定利益/損切率0.05以下だと、勝率が5割を切ります。ケリー基準の場合、勝率が5割を切ると勝負する価値がないとされ、損切率0.05(-5%)以下で設定するのは勝ち目がないと思います。これは、損切率0.05(-5%)以下だと売り買いのスプレッドの影響0.006(0.6%)が大きくなるため、負け越すのだと思います。
確定利益, 損切率が0.10(10%)以上だと勝率は55%を超えますが、確定・損切率0.1 (10%)以上となるような平均取引間隔は1回/3か月程度です。
確定利益rp, 損切率rl = 0.7 (70%)まで上昇させると、勝率が100%となります。これは、直近10年のTQQQのドローダウンが70%弱のため、負けなくなるためです。
損切なしの場合、当然、勝率は常に1(100%)になります。
上記から、損切率あり・超短期(1~数日)で勝率50%以上を目指すのは難しいと思われます。上昇トレンドのときのみ売買をすれば勝率が上昇すると思いますが、上昇トレンドを見極めるのは難しいと思います。
損切ありで勝率5割を超えるのは確定利益・損切率は0.1 (10%)以上となります。
取引1回あたり掛け金
下のグラフは資産を最大化する1回あたりの掛け金/資産比率です。

資産の何倍の掛け金で1回あたり投資するかを示したものです。
損切を行う場合、1回あたりの投資額を大きくすることができます。
optimal fを計算したところ、資金の1.6倍前後になりました。レバレッジをかけて1回値1.6倍程度掛けると資金の最大化が最速になるようです。
資産倍率
下のグラフは損切あり、損切なし、ガチホ、それぞれでの資産倍率です。
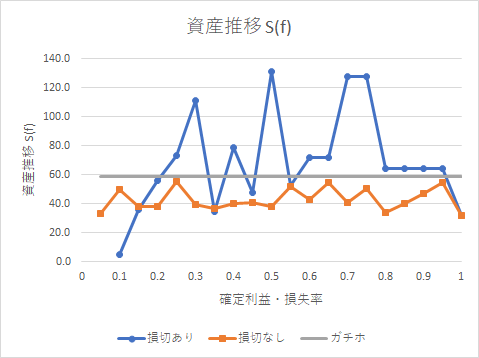
2010年年末にTQQQを一括購入し、2020年年末で保持した場合、上記灰色の線になります。資産は59倍になりました。
損切ありの場合, 0.05(5%上昇で確定、5%下落で損切)で運用すると、資産は約5倍でした。0.3~0.9(30%から90%上昇で利確、30%から90%下落で損切)までですと、ガチホの場合の59倍を上回りました。これはある程度の確率でロスカットを覚悟して、資金効率を上げていくと、どこかでガチホよりも利益が得られるということだと思います。
損切りなしの場合、0.05~1.0のいずれで確定させた場合においても資産は30~60倍程度となり、ガチホに及ばないまでも、それなりの利益を得ることができました。確定利益率を上昇させても、資産倍率は単調には伸びないため、常に優位な確定利益率はないということになります。そのため、例えば0.1(10%上昇で利確)などで適当に決めればよいと思います。
シミュレーション2
確定利益率Rp=0.03(3%上昇で利益確定)を固定し、損切率の条件を変えながら、ケリー基準に従った取引でのシミュレーションを行いました。
計算方法
- 投資対象:TQQQ
- 計算期間:2011年1月初めから2020年12月末まで
- TQQQの価格は始値->(高値or安値で始値に近い側)->(高値or安値で始値から遠い側)->終値で推移すると仮定。1分足データが入手できないため。
- ETF購入後、利確率まで上昇すれば、利益確定、損切率まで下落すれば損切する、を繰り返す。
- その際の1回あたりの掛け金はケリー基準に従う
- 確定後、翌日の始値で再度購入するとする。
- スプレッドは買い・売りともに0.03%とする。
- 利確率Rp=0.03(3%上昇で利益確定する)で固定とする。スプレッド込み3%上昇,スプレッド抜き2.4%で利益確定。(QQQで1%上昇に相当する上昇率で設定)
- 損切あり。損切レベルRl= -0.01~-1.0まで。
- 10年間繰り返した場合の勝敗記録から、それぞれの利確率、損切率の組み合わせについて、勝率pを求める(価格推移はランダムとされているので、得られた勝敗から勝率を求めても良いと考えている)。
- 勝率pからoptimal f, f= ((Rp+ 1) * p – 1) / Rlを求める。
- optimal fから1回あたりの最適掛け金を求める。
- 上記の場合での資産推移S(f)を確認する。
勝率
下記グラフは3%上昇で、利益確定、損切あり(-1%~-100%で損切)での勝率です。
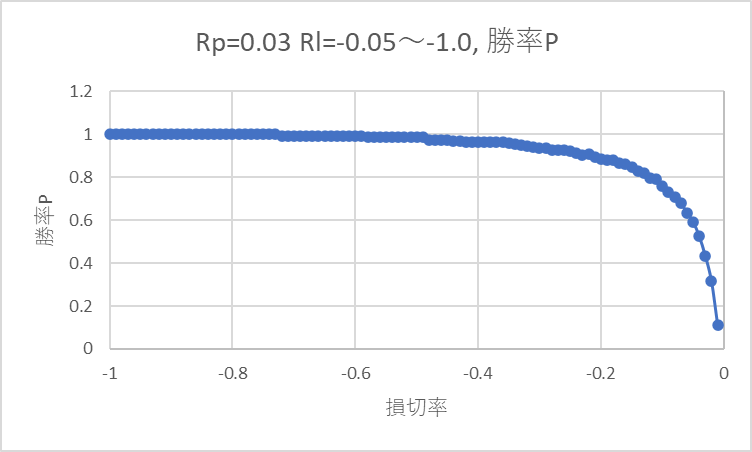
-0.01(-1%)~-0.04(-4%)で損切率を設定すると、勝率が5割を切り(確定より損切のほうが多い)、利益を上げられません。これはやはりスプレッドが0.6%あるため、損切率をシビアにすると負けやすくなるのだと思います。
-0.04(-4%)~-1.0(-100%)で損切すると勝率が5割を超えました。
-0.7(-70%)より低い値で損切設定すると勝率100%となりました。
取引1回あたり掛け金
下のグラフは3%上昇で利確し、0%~100%で損切した場合における、資産を最大化する1回あたりの掛け金/資産比率です。
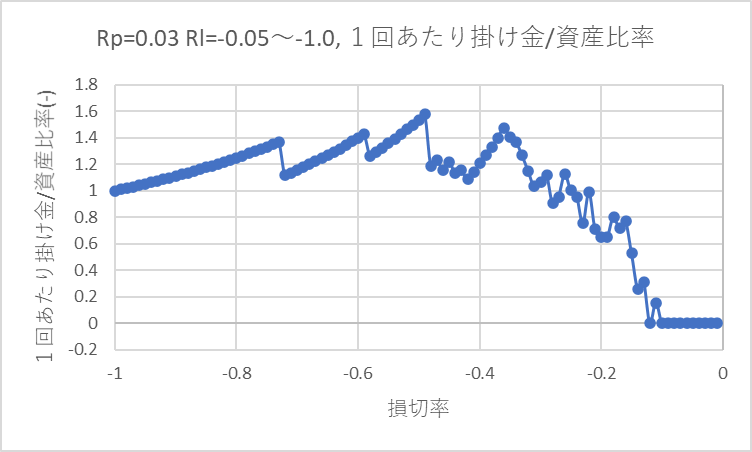
損切が~-0.1(10%下落で損切)の領域では掛け金0です。これは投資する価値がないということになります。
損切率-0.5(50%下落で損切)付近で資産を最大化する1回あたりの掛け金が最大の1.6倍になります。
実際に資産倍率が最大になるのは損切率-0.7(70%下落)で、このとき資産を最大化する1回あたりの掛け金は資産の1.4倍になります。(資産倍率は次項にて紹介しています)。
資産倍率
下のグラフは3%上昇で利益確定、損切あり(-1%~-100%で損切)での10年後の資産倍率です。
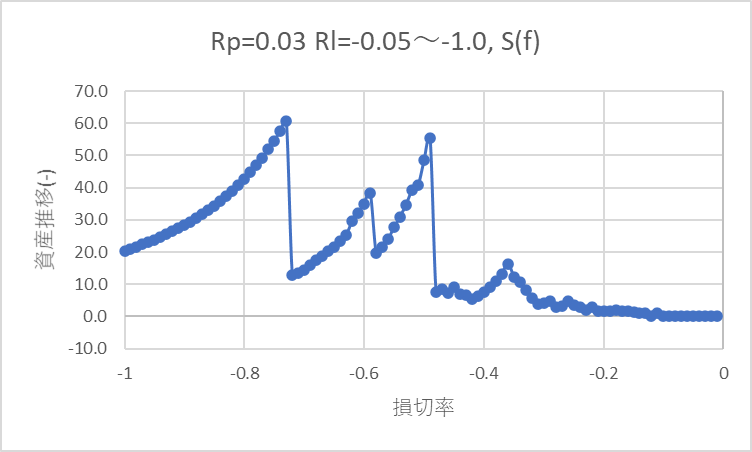
2010年年末にTQQQを一括購入し、2020年年末で保持した場合、資産は59倍でした。
3%上昇で利益確定し、損切なし(=-100%)で運用すると、資産は約20倍になりました。
損切率-0.7(70%下落で損切)の設定だと勝率100%なので、損切なしに比べ資金効率が上昇し、資産は60倍になりました。これは損切率を-0.7まで下げると損切率-1.0に比べ投資額が1.4倍まで上昇させられるからです。
-0.49(49%下落で損切)~-0.66 (66%下落で損切) に設定すると、資産20倍を上回る損切率が存在します。
例えば、損切率-0.5(50%下落で損切)とすると、資産は約56倍になります。これは、3%上昇で利益確定、損切なしでの資産上昇約20倍に比べ、大きく上回ります。しかし、損切率-0.7での資産60倍には及びませんでした。
このシミュレーションから、損切ありきではなく、過去の下落から損切しないであろうぎりぎりをロスカット基準に設定理すると利益が最大化しやすいと考えています。例えば、ロスカットを最高値から30%まで下落するあたりに設定するのが利益最大化すると考えています。
なお、今回は2011年~2020年でシミュレーションしました。別の期間でシミュレーションすれば当然異なる結果になると思います。
シミュレーション3
シミュレーション2に加えて、異なる利確率Rp=0.05(5%上昇で利確), Rp=0.10(10%上昇で利確)を追加しました。
計算方法
- 投資対象:TQQQ
- 計算期間:2011年1月初めから2020年12月末まで
- TQQQの価格は始値->(高値or安値で始値に近い側)->(高値or安値で始値から遠い側)->終値で推移すると仮定。1分足データが入手できないため。
- ETF購入後、利確率まで上昇すれば、利益確定、損切率まで下落すれば損切する、を繰り返す。
- その際の1回あたりの掛け金はケリー基準に従う
- 売却後、翌日の始値で再度購入するとする。
- スプレッドは買い・売りともに0.03%とする。
- 利確率Rp=0.03(3%上昇), R=0.05(5%上昇), Rp=0.10(10%上昇)の3種類。
- 損切あり。損切レベルRl= -0.01~-1.0(1%~10%下落)まで。
- 10年間繰り返した場合の勝敗記録から、それぞれの利確率、損切率の組み合わせについて、勝率pを求める(価格推移はランダムとされているので、得られた勝敗から勝率を求めても良いと考えている)。
- 勝率pからoptimal f, f= ((Rp+ 1) * p – 1) / Rlを求める。
- optimal fから1回あたりの最適掛け金を求める。
- 上記の場合での資産推移S(f)を確認する。
取引回数
下記グラフは確定利益率3%, 5%, 10%それぞれで、利益確定、損切率(-1%~-100%で損切)を変えたときの取引回数です。 縦軸は対数です。
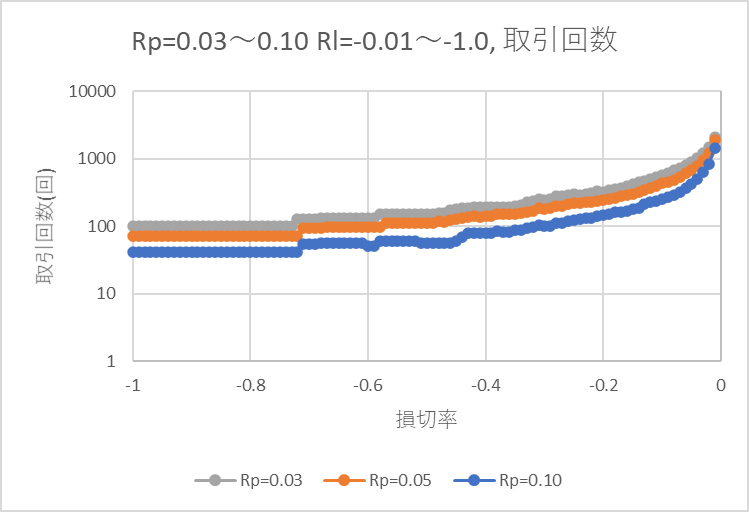
当然ですが、確定利益率が上昇すると、取引回数が下落します。
確定利益率3%, 損切率-100%(損切なし)のとき、取引回数は10年で102回でした。1年あたり10.2回になります。
勝率
下記グラフは確定利益率3%, 5%, 10%それぞれで、利益確定、損切率(-1%~-100%で損切)を変えたときの勝率です。
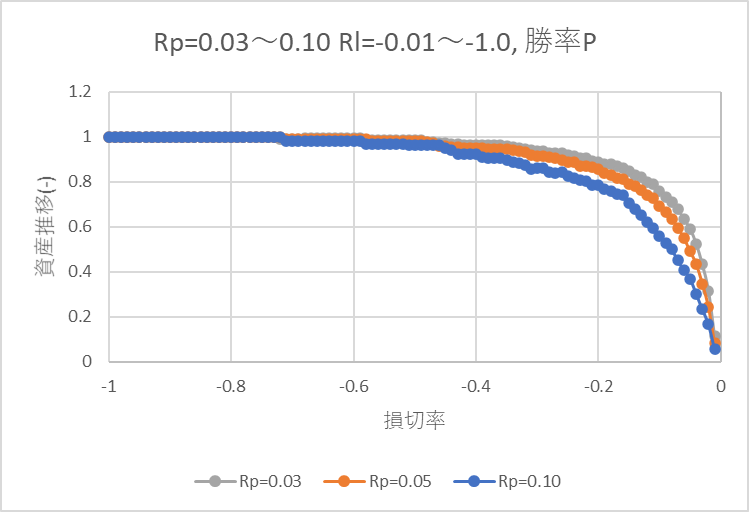
-0.10(-10%)~-1.0(-100%)で損切率を設定すると、どの確定利益率でも勝率が5割を超えました。
-0.7(-70%)より低い値で損切設定するとどの確定利益率でも勝率100%となりました。
取引1回あたり掛け金
下記グラフは確定利益率3%, 5%, 10%それぞれで、利益確定、損切率(-1%~-100%で損切)を変えたときの、資産を最大化する1回あたりの掛け金/資産比率です。
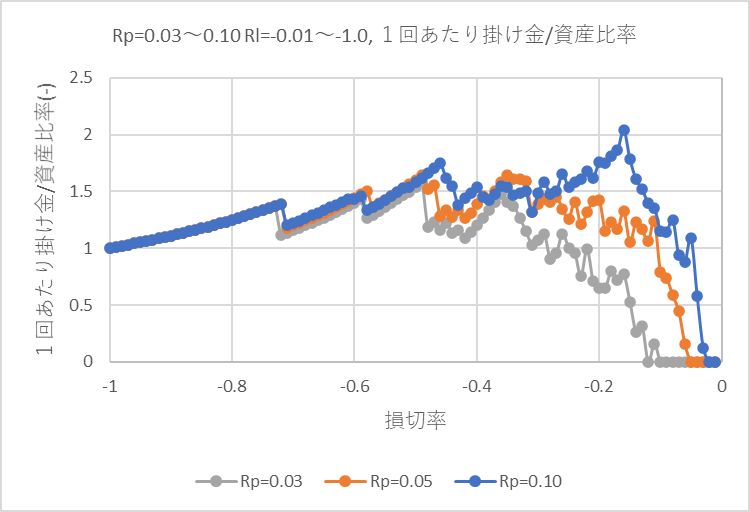
確定利益率が大きいほうが 損切が -0.1 ~-0.3(10~30%下落で損切)の領域で掛け金が大きくなります。これは掛け金を大きくしても資産を増やせるということです。
資産倍率
下記グラフは確定利益率3%, 5%, 10%それぞれで、利益確定、損切率(-1%~-100%で損切)を変えたときの、10年後の資産倍率です。
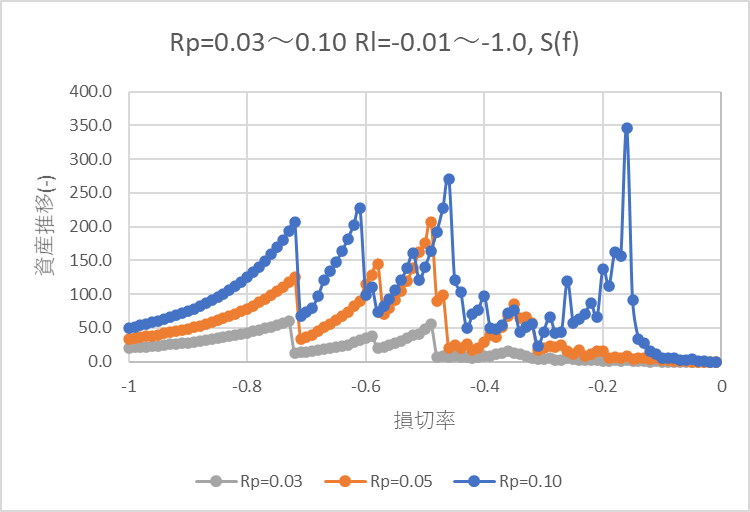
ベンチマークとしては、2010年年末にTQQQを一括購入し、2020年年末で保持した場合、資産は59倍でした。
全体的に確定利益率10%のほうが、3%, 5%に比べ資産倍率は大きくなりました。
確定利益率10%のとき、損切率-0.16(16%下落で損切)の設定だと資産が最大になりました。ただ、極値的に表れており、シミュレーション区間が変わると最適損切率は異なることが考えられます。
いずれの確定利益率においても、損切をしなくてすむ最大の損切率である-0.7(70%付近で損切)を上回る資産倍率となる損切率-0.1(10%下落で損切)~-0.7(で損切)の区間で見出すのは難しいと思います。
シミュレーション4
損切なしで確定利益率Rp=0.01(1%上昇で利確)~1.0(100%上昇で利確)での資産倍率をシミュレーションしました。
計算方法
- 投資対象:TQQQ
- 計算期間:2011年1月初めから2020年12月末まで
- TQQQの価格は始値->(高値or安値で始値に近い側)->(高値or安値で始値から遠い側)->終値で推移すると仮定。1分足データが入手できないため。
- ETF購入後、利確率まで上昇すれば、利益確定、損切率まで下落すれば損切する、を繰り返す。
- その際の1回あたりの掛け金はケリー基準に従う
- 売却後、翌日の始値で再度購入するとする。
- スプレッドは買い・売りともに0.03%とする。
- 利確率Rp=0.01(1%上昇)~Rp=1.0まで。
- 損切なし。損切レベルRl= -0.75、-1.0まで。
- 10年間繰り返した場合の勝敗記録から、それぞれの利確率、損切率の組み合わせについて、勝率pを求める(価格推移はランダムとされているので、得られた勝敗から勝率を求めても良いと考えている)。
- 勝率pからoptimal f, f= ((Rp+ 1) * p – 1) / Rlを求める。
- optimal fから1回あたりの最適掛け金を求める。
- 上記の場合での資産推移S(f)を確認する。
資産倍率推移
下記グラフは損切率-0.75, -1.0, 確定利益率1%~100%での10年後の資産倍率です。
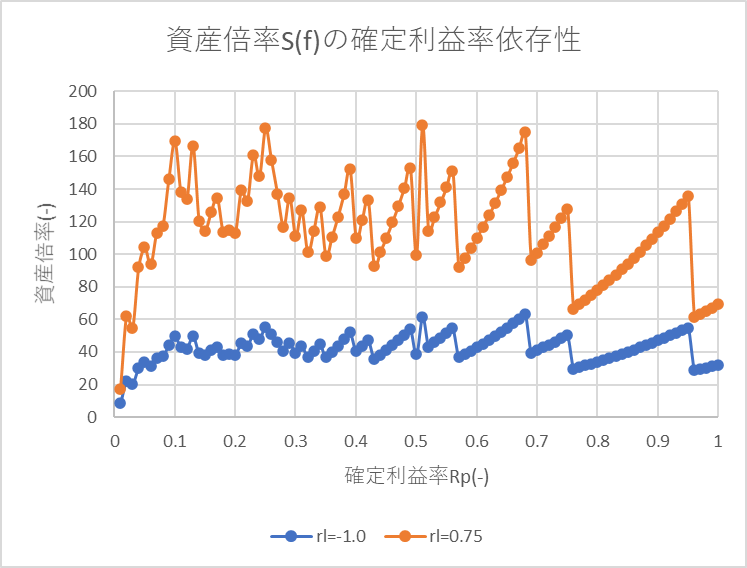
損切率-0.75(75%下落で損切)だと、実際には損切はありませんでした。なので、損切率を-0.75にすると損切率-1.0に比べ掛け金にレバレッジを1.33倍掛けることができるため、資産倍率が上昇します。
この結果を見ると、確定利益率0.1(10%上昇)までは資産倍率が上昇しますが、その後はランダムに動いているように見えます。
おそらく、利益率が0~0.05程度の低い間はスプレッド(買い・売りで0.006)の占める割合が大きいため資産倍率が低いと思います。
確定利益率が0.05~の範囲ではスプレッドの影響が小さくなって資産倍率が上昇します。ただし、0.1以上については、値動きとの相性で資産倍率が増えたり減ったりしているのだと思います。
この結果からすると、将来どのようにETF価格が推移するかわからないので、最適な確定利益率は0.1以上のどこかだろうが、正確にはわからないだろう、と考えています。
まとめ
最適な確定利益率は10%以上である可能性が高いと思います。確定利益率1~3%程度よりは5%~のほうが10年後の資産倍率は高くなると思います。10%~のどこかで最大化すると思いますが、どこで最大化するかはシミュレーション期間によっては変わる可能性があります。
損切率-0.1(10%下落で損切)~-0.7 (70%下落で損切) 程度にして損切を積極的に行い、掛け金を上昇させる場合と、損切しない場合を比較した場合、損切しない場合の資産倍率を上回る可能性は低いと思います。損切しないほうが資産は増える可能性が高いと思います。
損切しないぎりぎりに損切ラインを設定し、資金効率を最大化させるのが一番資産が増える可能性が高いと思います。



コメント